两个水壶相互倒水—水壶问题

Z.TIAN

Java/数据库

2018年4月27日

大约3.5k字

阅读需18分钟

本页文档最后更新于：2021年7月4日

点击此处快速跳到程序部分

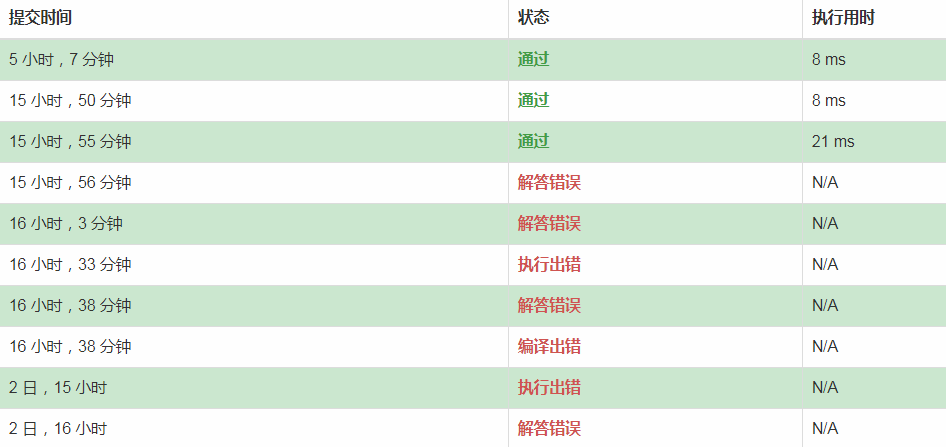
水壶问题

有两个容量分别为 x升和 y升的水壶以及无限多的水。请判断能否通过使用这两个水壶，从而可以得到恰好 z升的水？
如果可以，最后请用以上水壶中的一或两个来盛放取得的 z升水。

你允许：
装满任意一个水壶
清空任意一个水壶
从一个水壶向另外一个水壶倒水，直到装满或者倒空

示例1: (From the famous "Die Hard" example)
输入: x = 3, y = 5, z = 4
输出: True

示例2:
输入: x = 2, y = 6, z = 5
输出: False

第一印象

乍一看这道题目和题目的示例，以为直接用条件判断就能搞定，于是立刻写了如下非常错误的代码：

public boolean canMeasureWater(int x, int y, int z) {
    if( (0.5*x + 0.5*y == z)||(x + y == z)||
        (0.5*x + y == z)||(x + 0.5*y == z)||
        (x + x == z)||(y + y == z) ){
        return true;
    }else{
        return false;
    }  
}

当然执行的结果是错误的，这里主要烦了两个重要的错误：

杯子只能倒空或倒满，不能倒一半（像脑筋急转弯那样）
两个杯子，当然可以让水从一个倒入另一个

从上述一开始遇到的错误，可以引出此题的关键：

需要不断将水倒来倒去，从而利用容量差得到更多样的容量的水
为了减少实现复杂程度，输入的x，y应该按指定顺序，如前小后大
对特定情况，能提前排除就提前排除，比如（0,1,2）

进入正题

首先，是问题的抽象，该问题可以转化为问一个三元组r(x,y,z)，按一定规则对x，y进行运算，规则就是：

x，y只能被赋值不比自身大的数，
x，y运算过程中，只要有一个状态，或x，或y，或x+y，等于z，则问题得解
问题无解的条件？

然后，由特殊推普通，实际计算几个例子，看看有什么规律，杯子x，y每次的状态有：

注意：下面的每一步都是注定的，即‘只有这样操作才对目标的获得有意义’，
目标是什么？目标就是每次操作都要‘利用容量差产生更多样的容量的水’。

x=4  y=5
4    5              //初始状态
0    5              //小的倒空，大的倒满【问题I】
4    5-(4-0)=1      //大的将小的倒满，大的会剩余，这里剩余 1
0    1              //小的倒空
1    0              //大的中的剩余倒入小的
1    5              //大的倒满
4    5-(4-1)=2      //大的继续将小的倒满，大的还会剩余，这里剩余 2
0    2              //往复上述操作
2    0
2    5
4    5-(4-2)=3
0    3
3    0
3    5
4    5-(4-3)=4      //x==y，后续会再重新回到开始状态，故这是终止状态【问题II】
0    4
4    0
4    5

问题I，为什么小的倒空大的倒满？
因为如果相反，小的满，大的空，水只能从小杯子倒入大杯子，
且小杯子无剩余，故没有利用到容量差，所以这种顺序的操作时无意义的。 

问题II，如果x和y不相等，且y>x即剩余的水多于小杯子的容量怎么办？
答：此时归结为【第二种情况】后续会讲到，所以当 y<=x 时可当做【第一种情况】

初步的编码实现

由上述思路作指导，很自然的想到了使用递归这种方式，于是有了以下代码：

class Solution {
    public  int zx; 
    public  int sm; 
    public  int lg; 
    public  boolean MK = false; 
    public  boolean canMeasureWater(int x, int y, int z) {
        if(z == x||z == y||z==x+y||z==0) {
            return true;
        }
        if(z > x && z> y && z>(x+y)){
            return false;
        } 
        zx = z;
        sm = x;
        lg = y;
        if(x>y){
            int tp = sm;sm = lg;lg = tp;  
        }else{  
            recursion(sm,lg-(sm-0));
        }
        return MK;
    }
    public  void recursion(int x, int y){
        if(zx == x+y || zx == x || zx==y) 
            MK = true; 
        if(x <= y||y>zx){
            if(!MK) MK = false;
            return;
        }
        x = 0;
        if(zx == x+y || zx == x || zx==y)  
            MK = true;  
        int t = x;x = y;y = t; 
        x = x;
        y = lg;
        if(zx == x+y || zx == x || zx==y)  
            MK = true; 
        recursion(sm,lg-(sm-x));
    }
}

补全思路得到新的实现

上述代码不出意外的还是没过，解答出错，为什么呢，原来是原先的思路有问题，思考不全面，如下：

x=4  y=7
4    7
0    7
4    7-(4-0)=3
0    3
3    0
3    7
4    7-(4-3)=6      //上述步骤同先前同理
0    6              //但此时出现 大的里的剩余 比小的容量还大【问题I】
?    ?              
...

问题I 如果大杯子剩余的比小杯子容量大，怎么处理
答：此时应不同于一般情况，一般情况是大的里的剩余是比小的容量小
'所以剩余水可以倒入小的，但此时无法将大杯子的剩余水倒入小杯子，
因为会溢出，那么应该如何操作呢，本着利用‘容量差’的原则，所以：

需要将小杯子用大杯子的剩余水倒满，此时大杯子的水仍有剩余，
如果此时剩余的水还比小杯子的大，那么先倒空小杯子，
然后继续用剩余的水装满小杯子，直到剩余的水 小于小杯子容量，

此时停止，因为此时剩余的水可以倒入小杯子了，所以又回到了第一种情况。

下面，我们按刚才说的思路将先前的例子列完：

x=4  y=7
4    7
0    7
4    7-(4-0)=3
0    3
3    0
3    7
4    7-(4-3)=6      //此时，按刚才的思路【第二种情况】继续
0    6              //小杯子倒空
4    6-4=2          //用大杯子剩余的水倒满小杯子，大杯子还剩余 2
0    2              //此时回归【第一种情况】
2    0
2    7
4    7-(4-2)=5      //此时，又回到【第二种情况】
0    5
4    5-4=1          //此时又回归【第一种情况】
0    1
1    0
1    7
4    7-(4-1)=4      //此时xy相等，如果继续，则状态回归初始，故此时终止

上述例子即完整的展现了正确的迭代步骤，即需要分为【两种情况】，所以在先前递归形式的基础上，对每次的迭代中的 x y的大小分情况进入不同的迭代入口即可。然而这一新的实现仍然出错误了：Stack Overflow！

<< 更多精彩尽在『程序萌部落』>>
<< https://www.cxmoe.com >>

如何避免递归的栈溢出

对于溢出时的测试用例：22003,31237,137，在我本机跑时递归了九千次左右就溢出停止了，但对于一般的小的测试用例，答案已经都是正确的了，所以此时的思路应是正确的，只是实现形式有问题，需要优化！

重新对上一章节中说到的例子进行考究，发现真正有用的（跟Z比较判断的）状态其实只有如下：

x=4  y=7
4    7-(4-0)=3  //【情况一】
4    7-(4-3)=6       
4    6-4=2      //【情况二】      
4    7-(4-2)=5       
4    5-4=1           
4    7-(4-1)=4

优化情况二：按先前的思路可知，情况二其实不需要迭代操作，其就是在大杯子剩余水多于小杯子容量时，就拿小杯子每次都去装大杯子的剩余水，直到大杯子中剩余的水小于小杯子的容量，抽象为数学运算：

取余 y % x == c

实现上，由于需要中间的每个状态（和z比较），所以可以用while循环来完成，优化后的代码：
【情况一】：大水杯里的剩水不断的增加，直到增加到剩水大于小水杯容量；
【情况二】：大水杯剩水不断的减少，直到剩水小于小水杯的容量；
再次明确：情况一时小水杯的容量 >= 大水杯的剩水；情况二时小水杯的容量 < 大水杯的剩水；
注意：
对于每次迭代，都对两种情况分别对待，然后进行下一次迭代，此时迭代是靠递归驱动的。

class Solution {
    public static int zx; 
    public static int sm; 
  
    public static int lgt; 
    public static boolean MK = false; 
 
    public static boolean canMeasureWater(int x, int y, int z) {
        sm = x; lgt = y;
        if(x > y){
           sm = y; lgt = x; 
        }
        zx = z; 
        recursion(lgt);
        return MK;
    }
    //static int cnt = 0;
    public static void recursion(int rs) {
        if(sm + rs == zx|| sm + lgt == zx|| sm + rs == zx|| sm == zx|| rs == zx|| zx == 0){
            MK = true;
            return;
        }
        if(rs <= 0){
            if(!MK) MK = false;
            return;
        }
        if(sm <= rs){
            int tmp = rs;
            for(int i = 1; tmp >= sm;i ++){
                tmp = tmp - sm;
            }
            recursion(tmp); //情况一
        }else{
        
            int tmp = rs;
            for(int i = 1; tmp < sm;i ++){
                tmp = lgt - (sm - tmp);

            }
            recursion(tmp); //情况一
        }
    }
}

终极优化，递归的转化

上述代码仍然存在栈溢出的错误，所以还是递归的锅，显然，不是题目的测试样例刁钻，而是有些情况就是需要迭代几万次，即用递归是错误的实现方式。故转念一想，如何将递归转化为循环？

x=4  y=7
4    7-(4-0)=3  //【情况一】
4    7-(4-3)=6       
4    6-4=2      //【情况二】      
4    7-(4-2)=5       
4    5-4=1           
4    7-(4-1)=4

在此回顾上述的内容，发现其实代码中的递归已经没有复杂的处理逻辑，且退化成了驱动迭代的一种结构，所以显然可以改成循环。由于原递归可以连续执行，所以转为循环理所应当的最外层是 while(true)来制造连续迭代，然后循环的退出可以用return 或者break都可以，对于两种情况的处理还是要分别采用不同的实现，综上，去掉递归改用循环的代码：

public static boolean canMeasureWater(int x, int y, int z) {
    if(z == 0) return true;
    if((x == 0 || y == 0))
        return (x + y == z);
    if(x > y)
        int t = x; x = y; y = t;
    int rs = y;
    while(true){
        if(x + rs == z|| x + y == z|| x + rs == z|| x == z|| rs == z|| z == 0)
            return true;
        if(rs <= 0)
            return false;
        int tmp = rs;
        if(x <= rs){
            while(tmp >= x){
                tmp = tmp - x;
                //System.out.println((++cnt)+"\tb\tr("+x+","+tmp+")"+"\t"+z);
                if(x + tmp == z|| x + y == z|| x + tmp == z|| x == z|| tmp == z|| z == 0){
                    return true;
                }
            }
            rs = tmp;
        }else{
            while(tmp < x){
                tmp = y - (x - tmp);
                if(x + tmp == z|| x + y == z|| x + tmp == z|| x == z|| tmp == z|| z == 0){
                    return true;
                }
            }
            rs = tmp;
        }
    }
}

精益求精

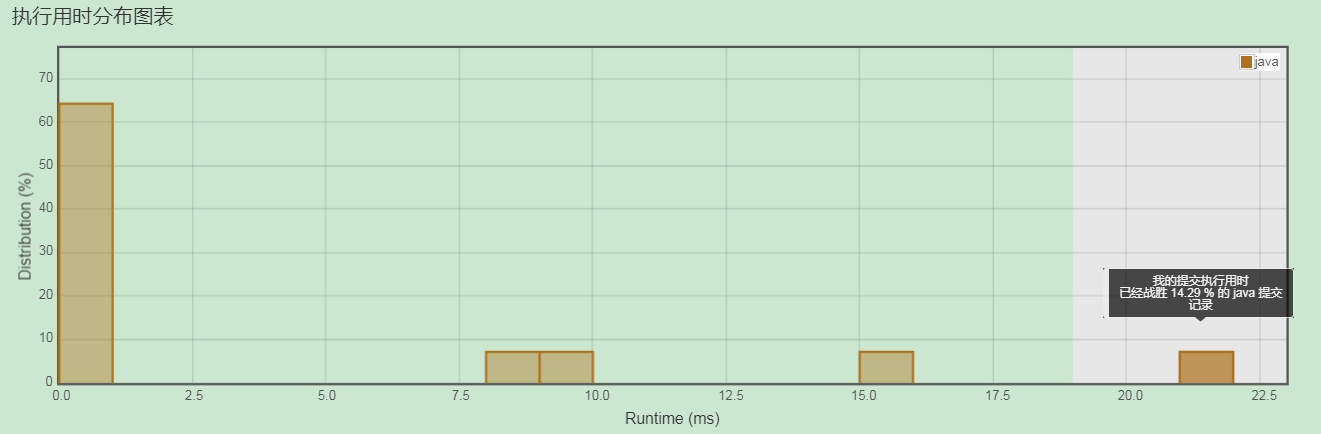
上述代码终于是得到了绿绿的通过，然而其执行速度却是最慢的，查看代码其实发现在判断停止的条件的语句上过于冗余了，然后有些变量还做了无畏的赋值，于是继续精简，最后得到如下代码：

public static boolean canMeasureWater(int x, int y, int z) {
    if(z == 0|| x + y == z) 
        return true;
    if((x == 0 || y == 0)) 
        return (x + y == z);
    if(x > y){
        int t = x; x = y; y = t;
    }
    int rs = y;  
    while(true){  
        if(rs <= 0) 
            return false;
        if(x <= rs){
            while(rs >= x){
                rs = rs - x;
                if( x + rs == z|| rs == z) 
                    return true;   
            }
        }else{
            while(rs < x){
                rs = y - (x - rs);
                if( x + rs == z|| rs == z) 
                    return true;
            }
        }
    }
}

上述代码的执行速度得到了不少的提升，由原先的21ms提升到了 8ms，如下图所示，现在下图提交的所有代码中，我的代码还成了第二个和第五个柱状图即8ms和21ms的样例程序，想想还有点小激动。

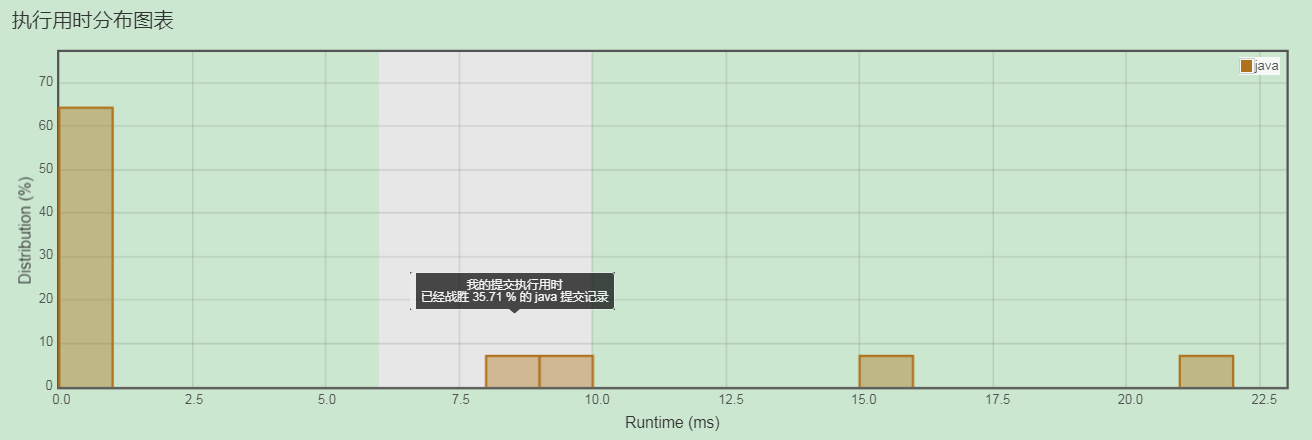
附第一梯队代码

当然，对于第一梯队的代码，使用到了 gcd() 函数对最大公约数进行求解，技巧性比较强，速度当然也快。相比之下，我这里其实相当于实现了一下gcd函数。但一般的小白（比如我）是很难将这个问题抽象成求解最大公约数的，所以我的思路其实更笨一点，但也更符合思考的逻辑。
下面是第一梯队的样例代码和解读。

class Solution {
    public boolean canMeasureWater(int x, int y, int z) {
        if (z==x+y || z==x || z==y || z==0)
            return true;
        if (x==0 || y==0 || z>x+y || z%gcd(x, y)!= 0)
            return false;
        return true;
    }
    private int gcd(int a, int b){
        return b == 0? a : gcd(b, a%b);
    }

}

此种题解的解题思路，转自网络

这道问题其实可以转换为有一个很大的容器，我们有两个杯子，容量分别为x和y，问我们通过用两个杯子往里倒水，和往出舀水，问能不能使容器中的水刚好为z升。那么我们可以用一个公式来表达：
z = m * x + n * y
其中m，n为舀水和倒水的次数，正数表示往里舀水，负数表示往外倒水，那么题目中的例子可以写成: 4 = (-2) * 3 + 2 * 5，即3升的水罐往外倒了两次水，5升水罐往里舀了两次水。那么问题就变成了对于任意给定的x,y,z，存不存在m和n使得上面的等式成立。根据裴蜀定理，ax + by = d的解为 d = gcd(x, y)，那么我们只要只要z % d == 0，上面的等式就有解，所以问题就迎刃而解了，我们只要看z是不是x和y的最大公约数的倍数就行了，别忘了还有个限制条件x + y >= z，因为x和y不可能称出比它们之和还多的水。

由于这道题前前后后想了两天多，且期间不断地修正自己的想法，修改对应的实现，最后AC。虽然只是一道普通的题目，但以前还真没真真正正的不借助参考的独立思考过这样难度的题目，所以就在这里啰嗦了一大堆，看来以后还是得多独立思考，正应那句话：“不是不会做，而是不去想” 啊！