用Python实现神经网络(待续)

• 介绍人工智能的基本概念和逻辑体系
• 研究两种数据的分类算法
• 使用Python运用分类方法实现只有一层的神经网络

分类两种类型

感知器，
适用性的线性神经元

使用Python的开发库：Pandas，Numpy，matplotlib：进行读取加工可视化

神经元

从交叉部分即神经末梢进行输入，在细胞核进行统一运算，然后通过轴突
传递到末尾，通过末尾的分叉传递到其他神经元

神经元的数学表示：

x：电信号
w：弱化系数（权重向量），表示神经元分叉部分对信号弱化的向量
x1->w1：从第一个管道传输时伴有的弱化
z：细胞核将全部电信号整合在一起

激活函数，又称单元步调函数
当z的值大于等于阈值时发送1，小于某阈值时发送-1
类似一个分类的函数，通常此函数比较复杂

向量的点乘（点积）：

矩阵的转置：

有了权重向量w，和训练样本x

1. 把权重向量初始化为0，或把每个分量初始化为【0,1】间得任意小数
2. 把训练样本输入感知器，得到分类结果-1或1
3. 根据分类结果更新权重向量w（反复输入更新，从而准确预测）

简化步调函数

添加w0和x0从而将判断直接转换为判断z的正负

权重的更新算法，

更新后的权重w：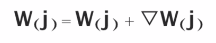

更新的增量：

y指的是输入的正确分类，y’感知器输出的分类
即如果分类正确，那么整个增量为零，分类错误才需要调整
系数n：模型的学习率，0~1，人为经验参数，需要使用者根据具体情况不断手动调整

权重更新示例：

得到了错误分类：

进行调整：




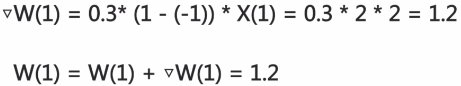
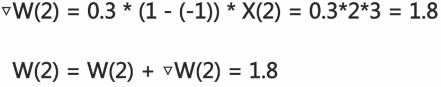
调整完成：

阈值更新：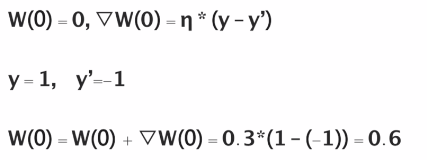

<< 更多精彩尽在『程序萌部落』>>
<< https://www.cxmoe.com >>

感知器的适用范围：

预测数据可以线性分割，不是A就是B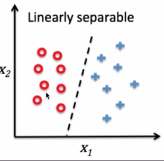

不适用于线性不可分割的数据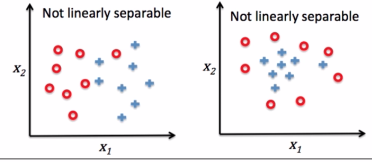

感知器分类算法的步骤：

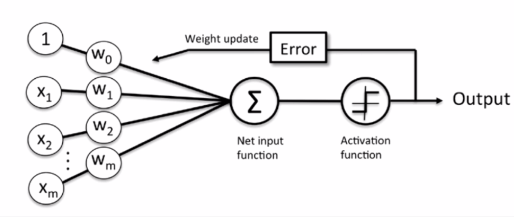
初始化训练样本x
初始化权重向量w
做点积
在步调函数/激活函数中进行判断
判断正确则输出，错误则更新权重w
做点积
在步调函数/激活函数中进行判断
判断正确则输出，错误则更新权重w
… …
… …
… …